지도 학습(Supervised Learning):
- 레이블이 있는 데이터로 학습합니다.
- 입력과 정답(레이블)이 쌍으로 제공됩니다.
- 모델이 입력을 통해 정답을 예측하도록 훈련합니다.
- 예: 이미지 분류, 숫자 인식, 텍스트 분류, 회귀 분석 등
- 회귀(Regression) 문제
- 목적: 연속적인 값을 예측하는 것
- 예시:
- 주택 가격 예측/주식 가격 예측/온도 예측/판매량 예측
- 알고리즘:
- 선형 회귀(Linear Regression)
- 다항 회귀(Polynomial Regression)
- 결정 트리 회귀(Decision Tree Regression)
- 신경망 회귀(Neural Network Regression)
- 성능 측정: MSE(Mean Squared Error), MAE(Mean Absolute Error), RMSE(Root Mean Squared Error) 등
비지도 학습(Unsupervised Learning)
비지도학습은 패턴을 학습하는거라고 볼수있는데 그럼 기준이 뭔지가 중요하겠다. 정답이라고 볼수 있는 기준말이다. 특히 클러스터링에서는 정확한 레이블이 없기 때문에 좋은 클러스터링의 기준을 정하는게 매우 중요하다. 그래서 클러스터링의 평가지표를 설정한다.
- 레이블이 없는 데이터로 학습합니다.
- 데이터의 패턴, 구조, 관계를 스스로 찾습니다.
- 예: 클러스터링(군집화), 차원 축소, 이상 탐지, 생성 모델 등
- 분류(Classification) 문제
- 목적: 데이터를 특정 범주나 클래스로 분류하는 것
- 예시:
- 이메일 스팸 필터링(스팸/정상)
- 이미지 분류(고양이/개 등)
- 질병 진단(양성/음성)
- 감정 분석(긍정/부정/중립)
- 알고리즘:
- 로지스틱 회귀(Logistic Regression)
- 의사결정 트리(Decision Tree)
- 랜덤 포레스트(Random Forest)
- 서포트 벡터 머신(Support Vector Machine)
- 신경망(Neural Networks)
- 성능 측정: 정확도(Accuracy), 정밀도(Precision), 재현율(Recall), F1 점수, ROC 곡선 등
클러스터링의 주요 특징:
- 데이터 포인트 간의 유사성/거리를 기반으로 그룹화
- 같은 클러스터 내 데이터는 서로 유사하고, 다른 클러스터의 데이터와는 차이가 있음
- 사전에 클러스터의 수나 구조를 명시적으로 알려주지 않아도 됨 (알고리즘에 따라 다름)
주요 클러스터링 알고리즘:
- K-means 클러스터링
- 가장 널리 사용되는 알고리즘
- 미리 클러스터 수(K)를 정해야 함
- 각 클러스터의 중심(centroid)을 기준으로 데이터 포인트를 할당
- 계층적 클러스터링(Hierarchical Clustering)
- 상향식(bottom-up) 또는 하향식(top-down) 접근 방식
- 덴드로그램(dendrogram)으로 클러스터 구조 시각화 가능
- DBSCAN(Density-Based Spatial Clustering)
- 밀도 기반 접근법
- 불규칙한 모양의 클러스터도 잘 찾아냄
- 노이즈 포인트 식별 가능
차원 축소(Dimensionality Reduction)는 비지도 학습의 중요한 기법 중 하나이다.
- 개념:
- 데이터의 특성(feature) 수를 줄이면서도 중요한 정보는 최대한 보존하는 기술
- 고차원(많은 특성)에서 저차원(적은 특성)으로 데이터를 변환
- 필요성:
- 차원의 저주(Curse of Dimensionality) 해결: 차원이 증가할수록 데이터가 희소해지면서 모델 성능이 저하됨
- 계산 효율성 향상: 적은 차원에서 더 빠른 계산 가능
- 데이터 시각화 용이: 2D나 3D로 축소하면 시각적으로 패턴 확인 가능
- 노이즈 제거: 불필요한 특성 제거로 신호 대 잡음비 개선
주요 차원 축소 기법:
- 주성분 분석(PCA: Principal Component Analysis)
- 가장 널리 사용되는 선형 차원 축소 기법
- 데이터의 분산을 최대한 보존하는 방향(주성분)으로 투영
- 상관관계가 있는 변수들을 서로 독립적인 성분으로 변환
- t-SNE(t-Distributed Stochastic Neighbor Embedding)
- 비선형 차원 축소 기법
- 고차원 공간의 유사한 데이터 포인트가 저차원에서도 가깝게 유지되도록 함
- 시각화에 특히 유용
- 오토인코더(Autoencoder)
- 신경망 기반 차원 축소 기법
- 입력 데이터를 재구성하는 과정에서 중간 층(병목 층)이 압축된 표현 학습
- 비선형 차원 축소 가능
- UMAP(Uniform Manifold Approximation and Projection)
- 최신 비선형 차원 축소 기법
- t-SNE보다 계산 효율성이 좋고 전역 구조도 더 잘 보존함
차원 축소는 데이터 전처리 단계로 자주 사용되며, 시각화, 클러스터링, 분류 등 다양한 머신러닝 작업의 성능을 향상시키는 데 도움된다.
일반화(Generalization)의 의미
일반화란 모델이 학습에 사용되지 않은 새로운 데이터에 대해서도 잘 동작하는 능력을 말합니다. 즉, 모델이 훈련 데이터에서 학습한 패턴을 기반으로 처음 보는 데이터에 대해서도 정확한 예측을 할 수 있는지를 나타냅니다.
일반화와 관련된 중요 개념
- 과적합(Overfitting):
- 모델이 훈련 데이터를 너무 잘 학습해서 그 데이터의 노이즈까지 학습한 상태
- 훈련 데이터에서는 성능이 매우 좋지만 새로운 데이터에서는 성능이 저하됨
- 일반화 능력이 떨어짐
- 과소적합(Underfitting):
- 모델이 훈련 데이터조차 충분히 학습하지 못한 상태
- 훈련 데이터와 새로운 데이터 모두에서 성능이 좋지 않음
- 일반화를 위한 기법:
- 정규화(Regularization)
- L1정규화 : 일부 가중치를 0으로 만들어 특성 선택효과를 보는 기법
- L2정규화 : 가중치를 작게 유지하도록 하는것
- 교차 검증(Cross-validation)
- 모델의 성능을 더 정확하게 평가하는 방법으로 Kfold cross validation이 있다. 데이터를 K개 그룹으로 나누고, 각 그룹을 한번씩 테스트 세트로 사용하며 나머지는 훈련세트로 사용하는거다. 이렇게 K번 학습과 평가를 반복하여 성능의 평균을 구한다.
- 데이터 증강(Data augmentation)
- 기존 데이터를 변형하여 더 많은 훈련 데이터를 만드는것
- 드롭아웃(Dropout)
- 학습 과정에서 무작위로 일부 뉴련을 비활성화 하여 모델이 특정 특성에 너무 의존하지 않도록 하는것
- 앙상블 학습(Ensemble learning)
- 정규화(Regularization)
좋은 기계학습 모델의 궁극적인 목표는 좋은 일반화 능력을 갖추는 것이다.
K-겹 교차 검증(K-fold Cross Validation)과 LOOCV(Leave-One-Out Cross Validation)
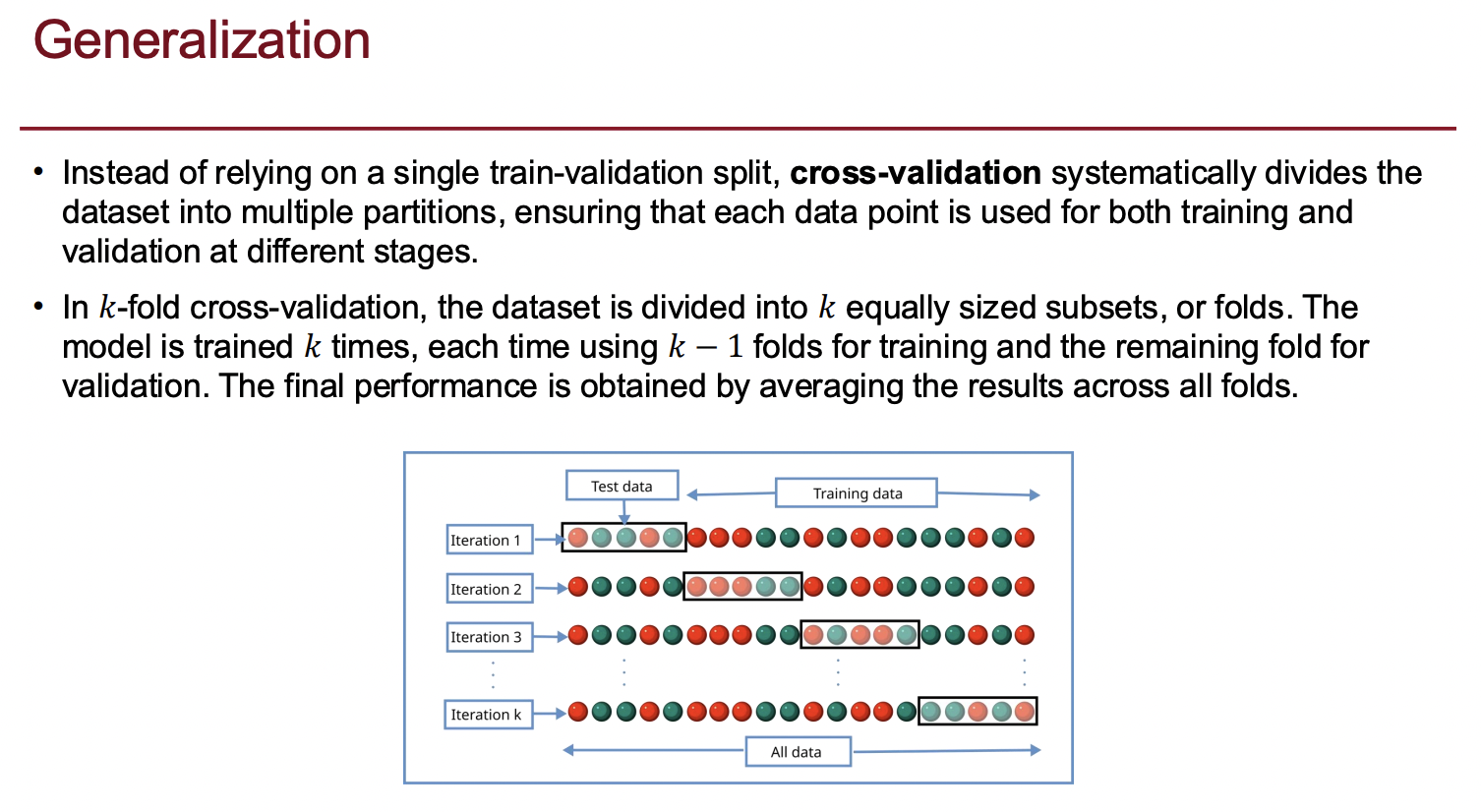
K-폴드 교차검증(K-fold Cross Validation) : 데이터를 K개 그룹으로 나누고, 각 그룹을 한번씩 테스트 세트로 사용하며 나머지는 훈련세트로 사용하는거다. 이렇게 K번 학습과 평가를 반복하여 성능의 평균을 구한다.
LOOCV(Leave-One-Out Cross Validation) : 데이터의 한 샘플만 테스트 세트로 사용하고 나머지는 훈련 세트로 사용한다. 이를 모든 샘플에 대해 반복한다. n개의 데이터가 있다면 n번 학습이 필요하므로 계산 비용이 높다. 데이터셋이 적을때 최대한 많은 데이터로 학습시키면서도 평가를 하고 싶을때 사용하게 된다. 그리고 LOOCV는 K폴드보다 bias가 적다. 왜냐면 거의 모든 데이터로 학습을 하기 때문이다.
Stratified K-fold는 K-fold 교차 검증의 중요한 변형이다. 이 방법은 특히 불균형 데이터셋(imbalanced dataset)에서 쓴다.
사용해야 하는 경우:
- 불균형 클래스 분포:
- 데이터셋에 클래스 불균형이 있을 때 (예: 90% 정상, 10% 비정상 사례)
- 일반 K-fold는 운이 나쁘면 특정 폴드에 소수 클래스가 전혀 없을 수 있음
- 작은 데이터셋:
- 데이터 크기가 작을 때 클래스 비율 유지가 더욱 중요함
- 희귀 클래스 존재:
- 의료 진단, 사기 탐지 등 희귀하지만 중요한 클래스가 있는 경우로 이런 불균형 데이터셋에 일반 Kfold교차 검증을 사용하면 어떤 폴드에는 희귀 클래스의 샘프링 거의 또는 전혀 포함되지 않을수 있다. 이런 문제를 해결하기 위해 stratified K-fold를 사용한다.
- 정상거래는 99.9% , 사기 거래는 0.1%
- 건강한 환자는 95%, 특정 질병환자 5%
- 정상에미일 80%, 스팸이메일 20%
- 의료 진단, 사기 탐지 등 희귀하지만 중요한 클래스가 있는 경우로 이런 불균형 데이터셋에 일반 Kfold교차 검증을 사용하면 어떤 폴드에는 희귀 클래스의 샘프링 거의 또는 전혀 포함되지 않을수 있다. 이런 문제를 해결하기 위해 stratified K-fold를 사용한다.
Stratified K-fold의 각 폴드에서는 희귀 클래스의 비율이 모두 약 10%로 유지됩니다. 즉, 모든 폴드가 원래 데이터셋의 클래스 분포를 유지한다.
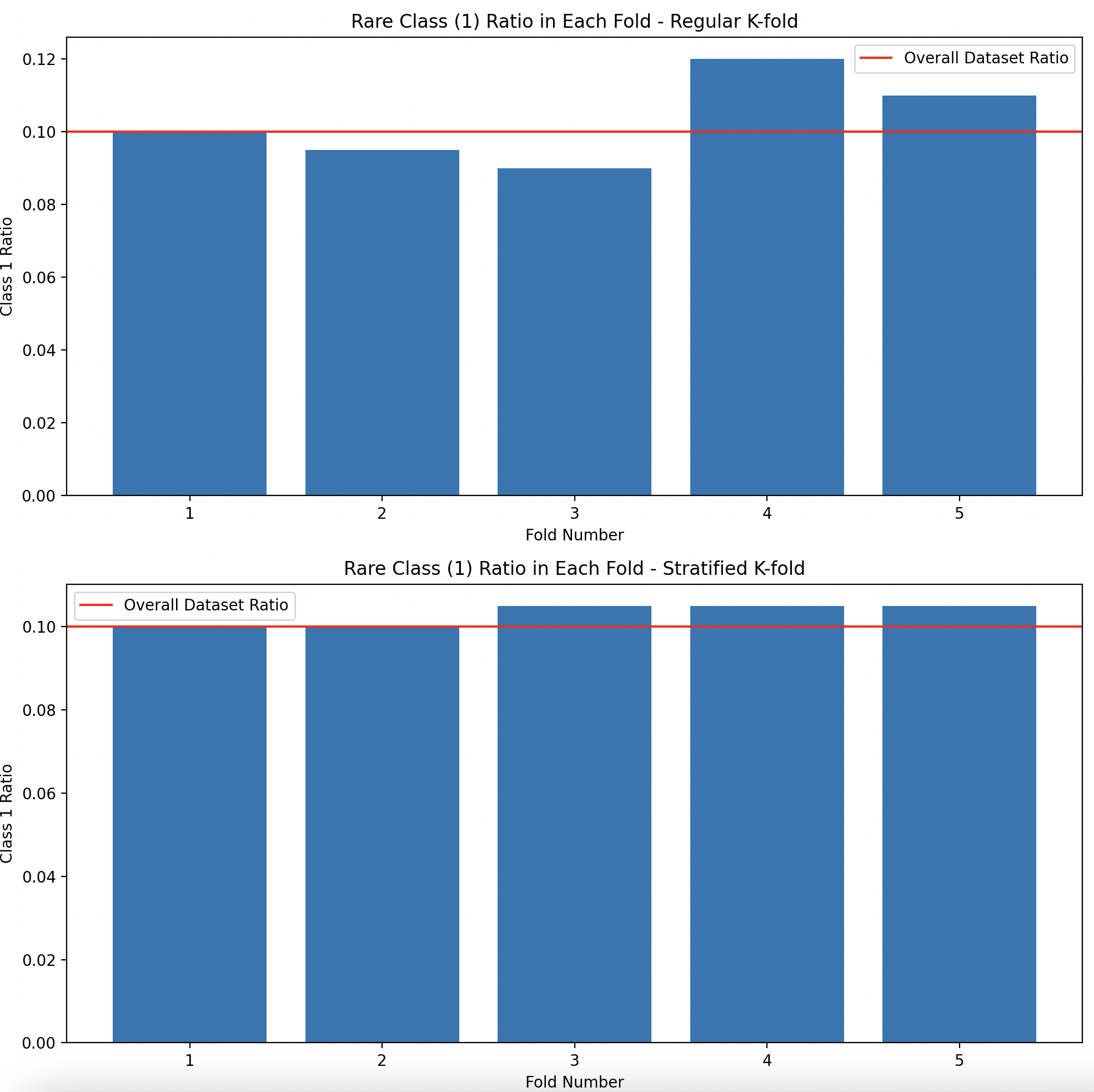
scikit-learn의 cross_val_score 함수도 분류 문제에서는 기본적으로 Stratified K-fold를 사용한다. 더 안정적인 겨로가를 제공하기 때문에 대부분 분류문제에에서 stratified Kfold를 선호한다.
import numpy as np
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
# 불균형 데이터셋 생성
X, y = make_classification(
n_samples=1000,
n_classes=2,
weights=[0.9, 0.1], # 클래스 0: 90%, 클래스 1: 10%
random_state=42
)
# 클래스 분포 확인
print(f"클래스 0 샘플 수: {sum(y == 0)}")
print(f"클래스 1 샘플 수: {sum(y == 1)}")
# 일반 K-fold와 Stratified K-fold 비교
kf = KFold(n_splits=5, shuffle=True, random_state=42)
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# 각 폴드에서의 클래스 분포 계산
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))
# 일반 K-fold
fold_ratios_kf = []
for i, (_, test_index) in enumerate(kf.split(X)):
fold_class_1 = sum(y[test_index] == 1)
fold_total = len(test_index)
fold_ratio = fold_class_1 / fold_total
fold_ratios_kf.append(fold_ratio)
print(f"일반 K-fold - 폴드 {i+1}: 클래스 1 비율 = {fold_ratio:.2f}")
# Stratified K-fold
fold_ratios_skf = []
for i, (_, test_index) in enumerate(skf.split(X, y)):
fold_class_1 = sum(y[test_index] == 1)
fold_total = len(test_index)
fold_ratio = fold_class_1 / fold_total
fold_ratios_skf.append(fold_ratio)
print(f"Stratified K-fold - 폴드 {i+1}: 클래스 1 비율 = {fold_ratio:.2f}")
# 그래프로 시각화
ax1.bar(range(1, 6), fold_ratios_kf)
ax1.set_title('일반 K-fold의 각 폴드별 희귀 클래스(1) 비율')
ax1.set_xlabel('폴드 번호')
ax1.set_ylabel('클래스 1 비율')
ax1.axhline(y=0.1, color='r', linestyle='-', label='전체 데이터셋에서의 비율')
ax1.legend()
ax2.bar(range(1, 6), fold_ratios_skf)
ax2.set_title('Stratified K-fold의 각 폴드별 희귀 클래스(1) 비율')
ax2.set_xlabel('폴드 번호')
ax2.set_ylabel('클래스 1 비율')
ax2.axhline(y=0.1, color='r', linestyle='-', label='전체 데이터셋에서의 비율')
ax2.legend()
plt.tight_layout()
plt.show()'ML&AI' 카테고리의 다른 글
| 벨만 최적 방정식(Bellman Optimality Equation) (1) | 2025.03.21 |
|---|---|
| 강화학습 Markov Decision Process (0) | 2025.03.21 |
| 강화학습Reinforcement learning 데이터셋을 미리 준비하지 않고, 환경과 상호작용하면서 데이터를 수집하고 학습 (0) | 2025.03.12 |
| 웹 기반 코퍼스 분석 도구 / 유사도 기반의 저자판별 (2) | 2024.11.12 |
| 텍스트마이닝 (1) | 2024.10.20 |



